poymeeting.blogg.se - How to estimate the simple linear regression equation in r

How to estimate the simple linear regression equation in r how to#

The simple linear regression is used to predict a continuous outcome variable (y) based on one single predictor variable (x). A non-zero beta coefficients means that there is a significant relationship between the predictors (x) and the outcome variable (y). Once, the beta coefficients are calculated, a t-test is performed to check whether or not these coefficients are significantly different from zero. This method of determining the beta coefficients is technically called least squares regression or ordinary least squares (OLS) regression. Mathematically, the beta coefficients (b0 and b1) are determined so that the RSS is as minimal as possible. Since the mean error term is zero, the outcome variable y can be approximately estimated as follow: This is one the metrics used to evaluate the overall quality of the fitted regression model. The average variation of points around the fitted regression line is called the Residual Standard Error ( RSE). The sum of the squares of the residual errors are called the Residual Sum of Squares or RSS. Some of the points are above the blue curve and some are below it overall, the residual errors (e) have approximately mean zero. the error terms (e) are represented by vertical red linesįrom the scatter plot above, it can be seen that not all the data points fall exactly on the fitted regression line.the intercept (b0) and the slope (b1) are shown in green.the best-fit regression line is in blue.The figure below illustrates a simple linear regression model, where: Note that, b0, b1, b2, … and bn are known as the regression beta coefficients or parameters.

How to estimate the simple linear regression equation in r how to#

how to assess the performance of the model.

how to make predictions of the outcome of new data,.

how to compute simple and multiple regression models in R,.

the basics and the formula of linear regression,.

Make predictions using the test set and compute the model accuracy metrics.

Build the regression model using the training set.

Randomly split your data into training set (80%) and test set (20%).

The higher the R2, the better the model.Ī simple workflow to build to build a predictive regression model is as follow:

R-square, representing the squared correlation between the observed known outcome values and the predicted values by the model.

The lower the RMSE, the better the model. RMSE is computed as RMSE = mean((observeds - predicteds)^2) %>% sqrt(). It corresponds to the average difference between the observed known values of the outcome and the predicted value by the model.

Root Mean Squared Error, which measures the model prediction error.

Two important metrics are commonly used to assess the performance of the predictive regression model:

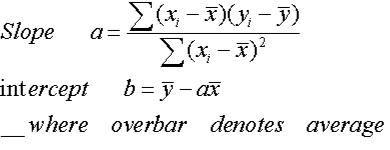
In other words, you need to evaluate how well the model is in predicting the outcome of a new test data that have not been used to build the model. When you build a regression model, you need to assess the performance of the predictive model. Once, we built a statistically significant model, it’s possible to use it for predicting future outcome on the basis of new x values. The goal is to build a mathematical formula that defines y as a function of the x variable. Linear regression (or linear model) is used to predict a quantitative outcome variable (y) on the basis of one or multiple predictor variables (x) (James et al.